Aim 🥅
Understand the transformer architecture and its components. Deeply analyze the paper "Attention is all you need" and its components.
TL;DR 🩳
- An insane analysis of my most feared paper, Attention is all you need.
- Shit ton of math, but in simple words, matrices are awesome.
- We have an encoder and a decoder stack with equal layers of encoders and decoders.
- The text first goes to word embedding step and then positional data is fed in to these embedding vectors.
- Post that it goes through a series of encoders and then through a series of decoders where the magic happens:
- Encode has a self attention layer and a feed forward layer
- Self attention is how much a word is relevant to the current context (sentence or paragraph whatever), precisely to know it's value
- For self attention we have 3 matrices that have to be multiplied with the vectors to get 3 new vectors, Query, Key and Value
- Query: “Which other words in the sequence are relevant to me?”
- Key: like a label that helps the model identify how a word might be relevant to other words in the sequence.
- Value: The value vector holds the actual word content information.
- For self attention we have 3 matrices that have to be multiplied with the vectors to get 3 new vectors, Query, Key and Value
- Now the code flows from self attention to feed forward and goes on and on till it comes out of the encoder stack
- Then it goes to decoder, first a new Key and Value is measured which goes to each of
encoder-decoder attention layer, this layer resides in middle of the decoder with self attention -> encoder decoder attention -> feed forward layer
- At last a linear layers turns those random looking vectors into probabilities for the next word to be placed
- And our softmax layer select the word to be shown at the end, mostly with the highest probability
- Yeah it's also called beast with many heads due to multi headed self attention, idk why do we even have such shit lol, math in this was cool, the matrices and all, but there were so many unknowns giving me fomo lol
What's on the plate 🍽?
-
Check 111 Visualizing A Neural Machine Translation Model - Sequence to Sequence model and 110 Recurrent Neural Networks and 000 Deep Learning and Neural Networks
-
There is one encoding and one decoding component,
- both receive a list of vectors and
- throw out vectors post processing
- len(encoders) == len(decoders)
-
Encoder is then broken down into a
Self-Attentionlayer and aFeed Forward Neural Networklayer. While the decoder has a specialEncoder-Decoder Attentionlayer in the middle of the other two.- encoder and decoder
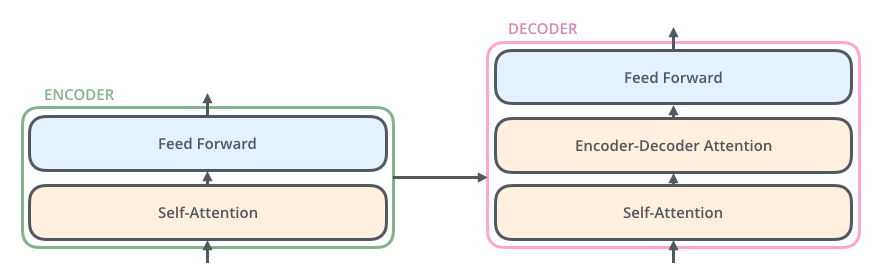
- encoder and decoder
-
One key property of transformer is that word in each position flows through its own path in the encoder. There are dependencies between these paths in self attention layer, while feed forward layer does not have them, so various paths can be executed in parallel. It goes like this from one encoder to another
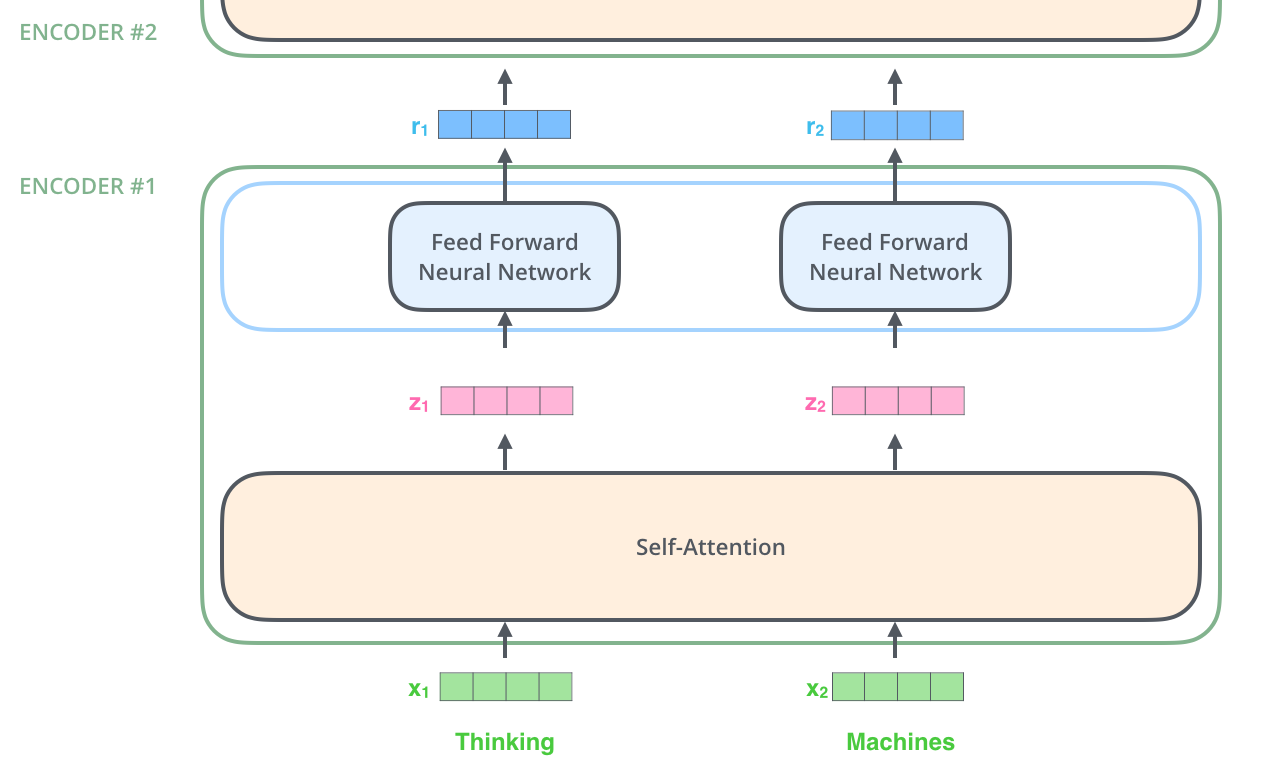
-
Self-Attention is a very important term here. Let's dig deeper
-
Say I have this sentence:
The animal didn't cross the street because it was too tired -
So
"it"here means what? animal or the street? humans can easily say"it"refers to animal here. But machines can't, so self-attention allows the model to associate"it"with"animal" -
OK so how does it work?
- We have to create 3 vectors from each of encoder's input vectors (here input vectors are nothing but word embeddings),
- these 3 vectors are created by multiplying the embedding with 3 matrices which were trained during the training process
- Query vector q1: “Which other words in the sequence are relevant to me?”
- Key vector k1: like a label that helps the model identify how a word might be relevant to other words in the sequence.
- Value vector v1: The value vector holds the actual word content information.
- Generally these new vectors are low dimensional (64 here for 512 word embedding)
- It looks like this:
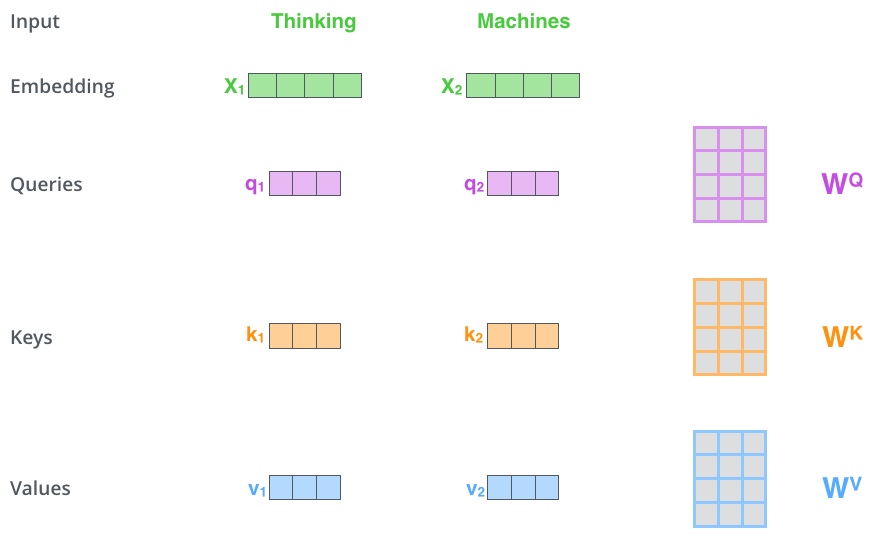
- It looks like this:
- Well what is this query, key and value vectors?
- well these are abstractions useful for calculating and thinking about attention, step 2 will clarify this!
- these 3 vectors are created by multiplying the embedding with 3 matrices which were trained during the training process
- In step 2, we calculate a score, we need to score each word of input vector against the word embedding under consideration
- score: determines how much focus to place on other parts of the input sentence as we encode a word at a certain position.
- score is dot product of query and key vector of the respective word we are scoring
- like this:
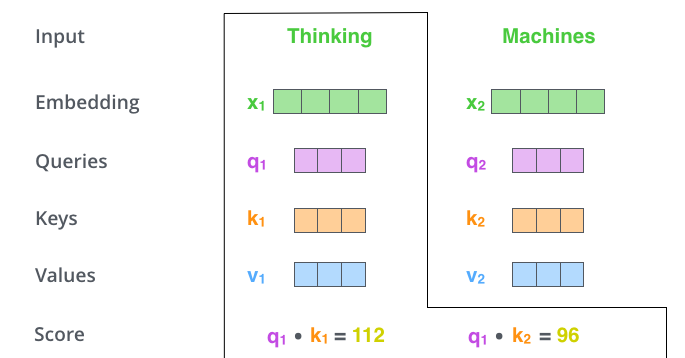
- like this:
- and 4. Divide scores by 8 (square root of dimension of the key, query and value vector which was 64 in our case, so sq root 64 is 8).
- then pass the result through a softmax operation. Softmax normalizes the score so they are all positive and add up to 1
- step 3 and 4:
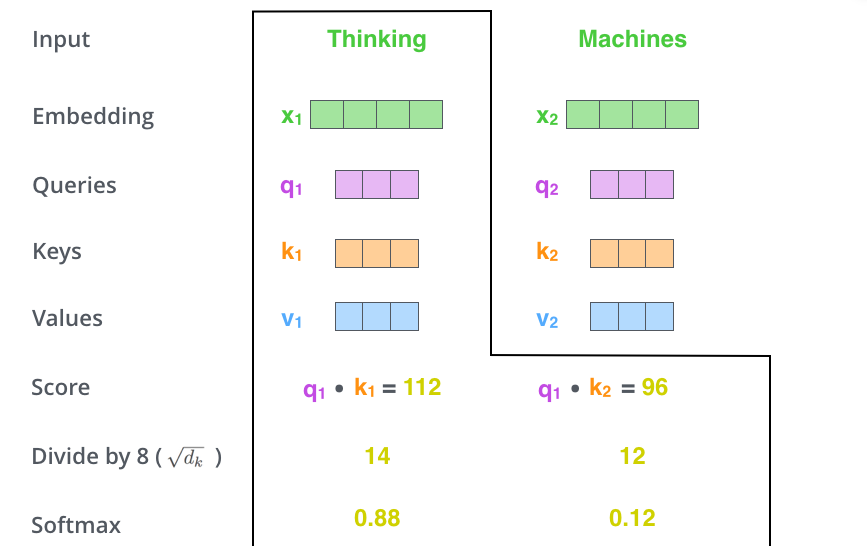
- step 3 and 4:
- Softmax tell how much each word is expressed at this position, so for position 1, obviously word 1 has to have the highest softmax value
- then pass the result through a softmax operation. Softmax normalizes the score so they are all positive and add up to 1
- Multiply each value vector by the softmax score, this is to remove irrelevant words with less value
-
Sum up the weighted value vectors. This produces the output of self-attention layer at this position (for the first word):
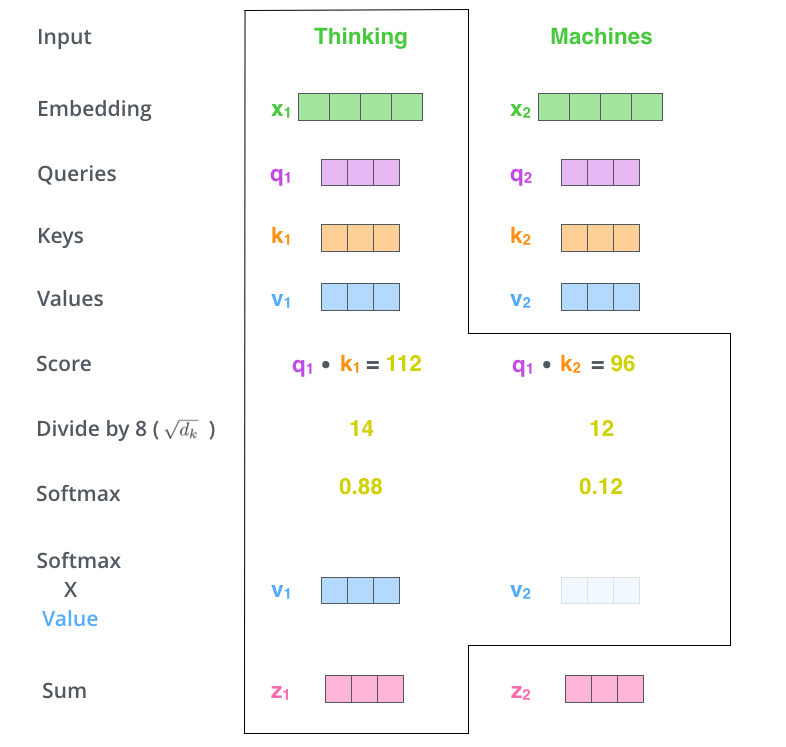
- This is how we get the vector which can be sent to the feed forward neural network, now all can run in parallel. In real machine, this calculation is done at matrix form for faster processing.
- We have to create 3 vectors from each of encoder's input vectors (here input vectors are nothing but word embeddings),
-
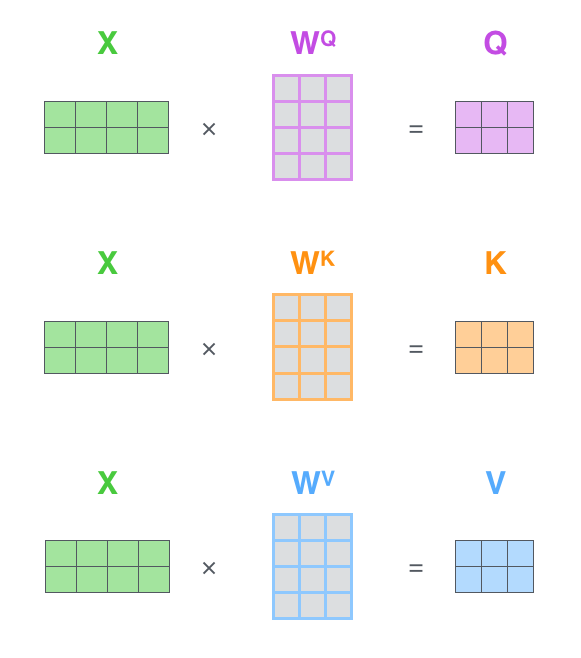
All this calculation in matrix form is very simple if you pay attention, each row of X here resemble a word embedding and simple matrix multiplication:
- finding clubbed Q, K and V, clubbed as in for all the input embeddings:
- The rest of steps from 2 to 6 can be put in this math formula, very simple indeed:
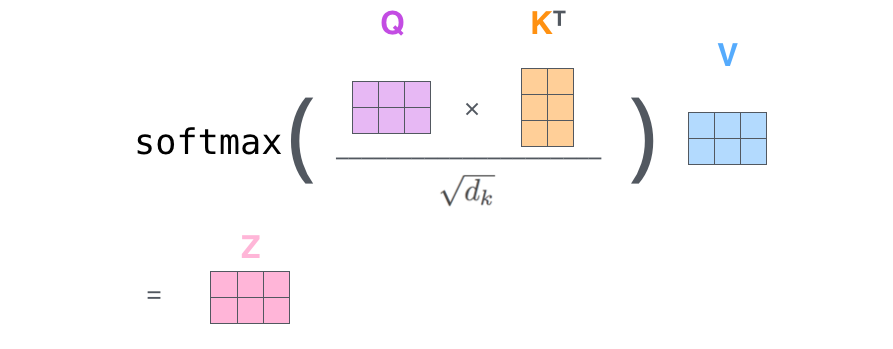
- finding clubbed Q, K and V, clubbed as in for all the input embeddings:
-
Beast with many heads!
Basically this give the model a richer representation of the input sequence. It allows the model to handle complex language patterns and long-range dependencies.
- Now along with self-attention, the paper talks about
multi-headed attention. This improves the performance in two ways:- Expands model's ability to focus on different positions
- It gives the attention layer multiple
representation subspaces. In multi headed attention, we have multiple sets of Query/Key/Value weight matrices.{8 heads for this example}Each set of this is randomly initialized, Then, after training, each set is used to project the input embeddings (or vectors from lower encoders/decoders) into a different representation subspace.
- Model thinks with different heads, so different weight matrices too:
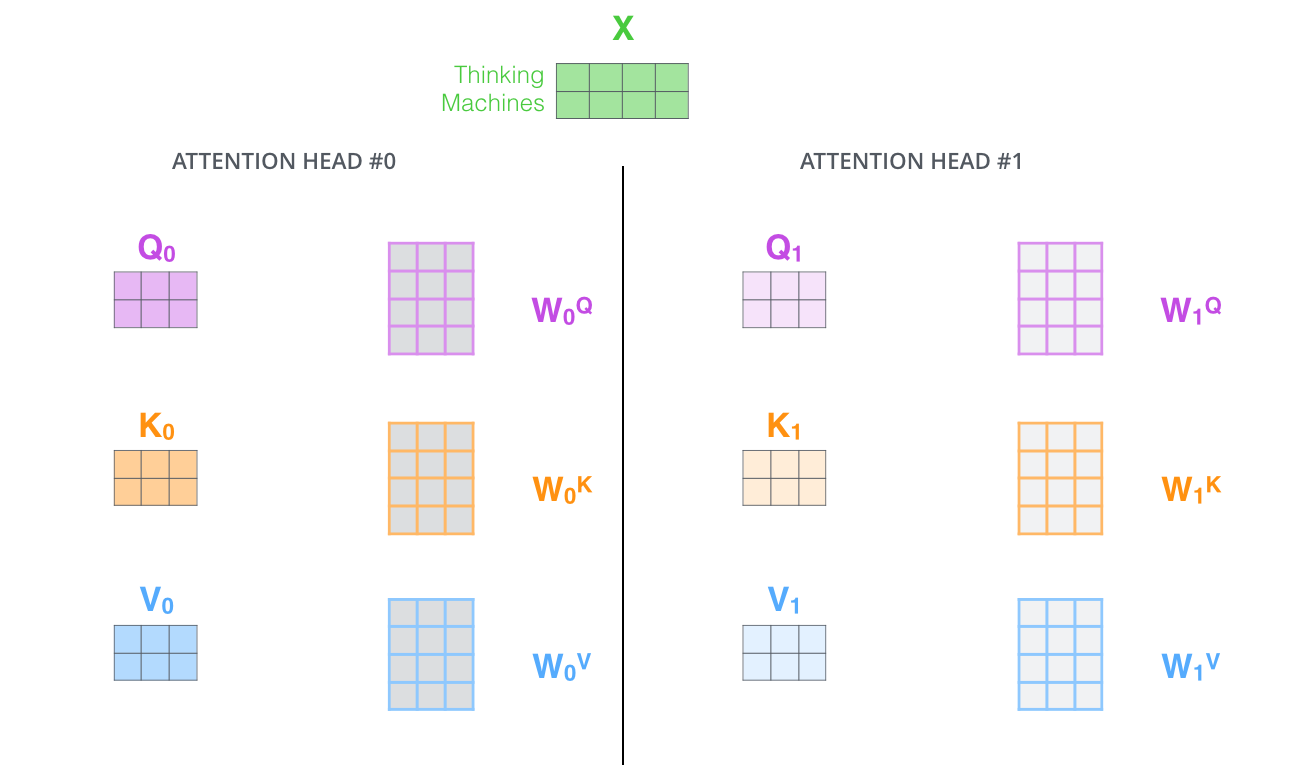
- So if we do the same self-attention calculation 8 times with different weight matrices, we would get 8 different z matrices. But the feed forward layer does not expect 8 matrices, instead a single matrix with a vector for each word as a row in it.
- So let's make these 8 matrices to 1, we concat the matrices, then multiply them by an additional weight matrix WO.
- Looks like this:
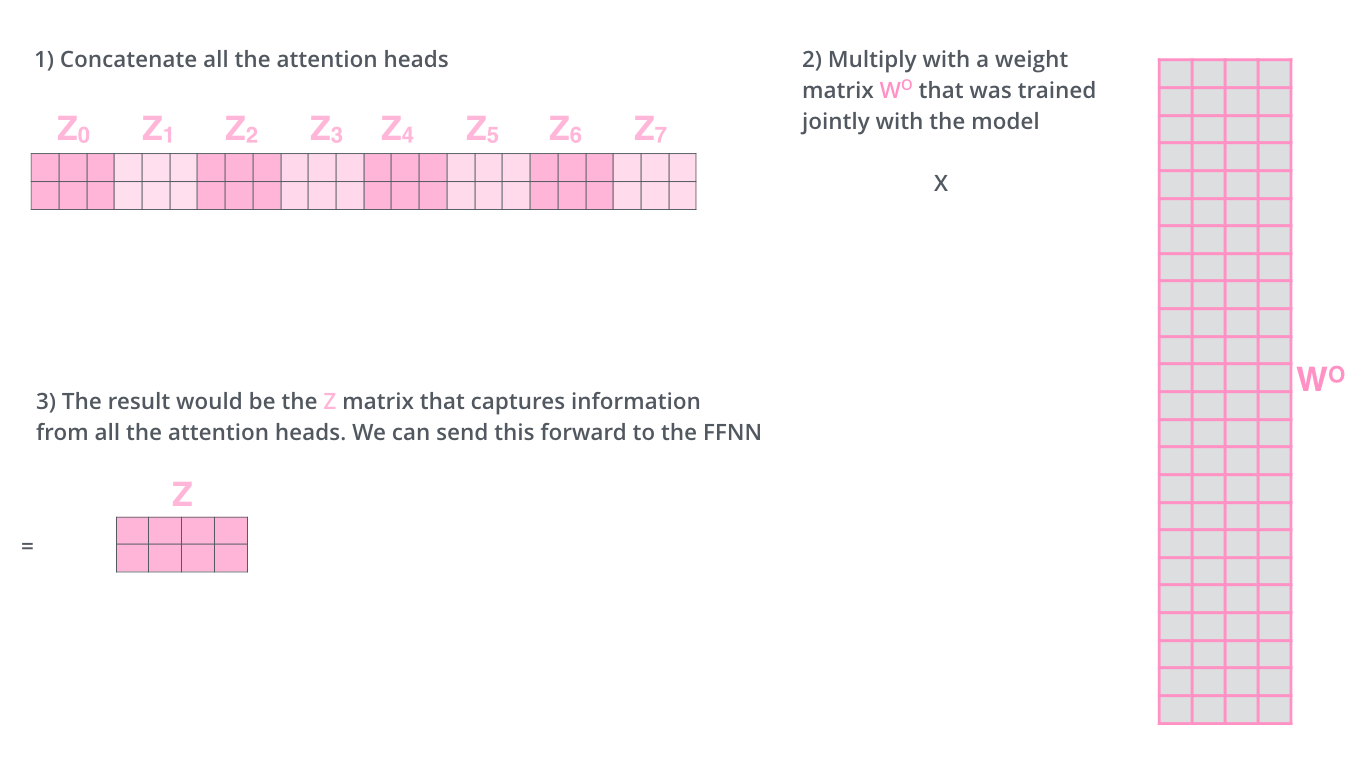
- Looks like this:
- In a nutshell, this process looks like this:
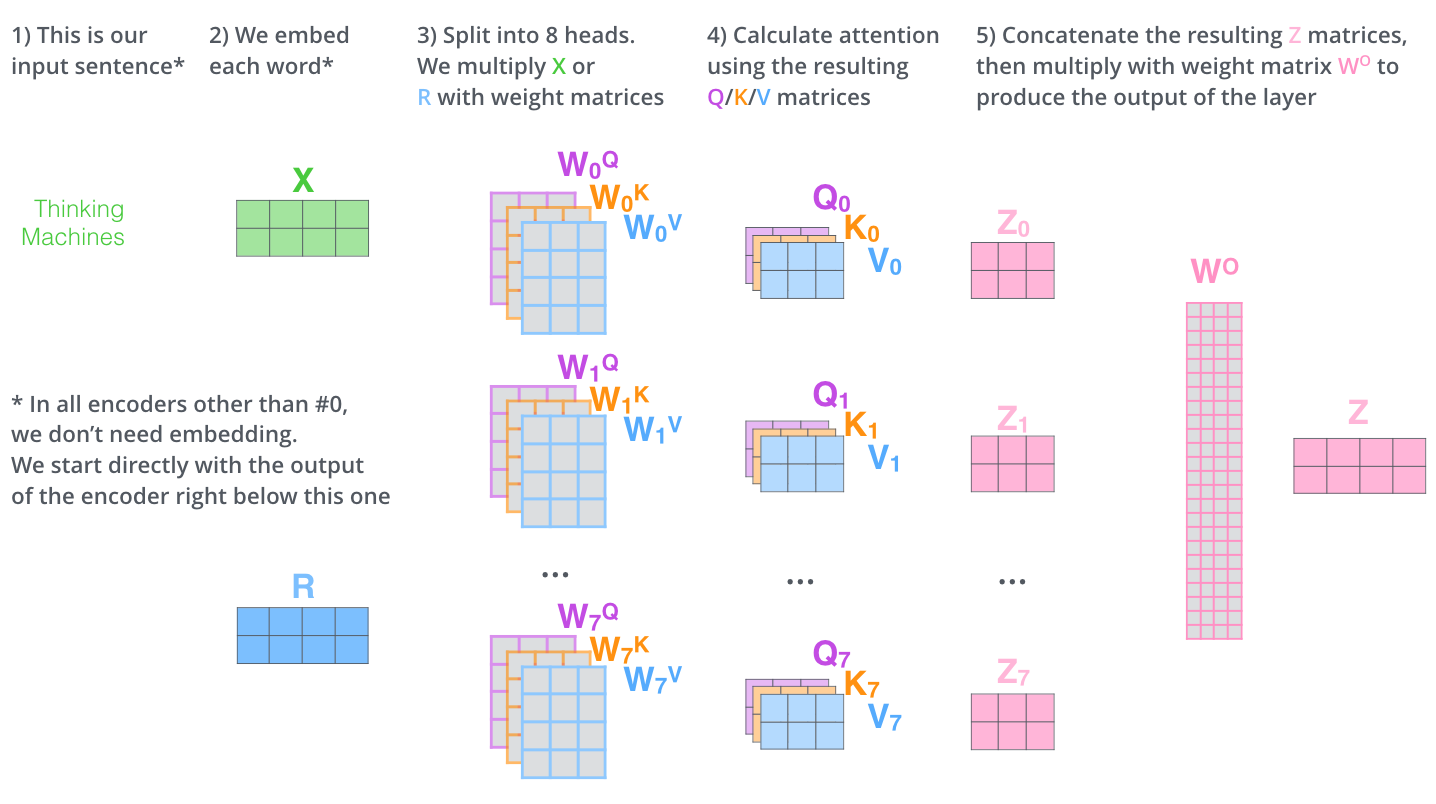
Positional encoding remains!
- A way to account for order of words in the input.
- Transformer adds a vector to each input embedding. Model learns the pattern of these added vectors to determine position of each word.
- Looks like this:
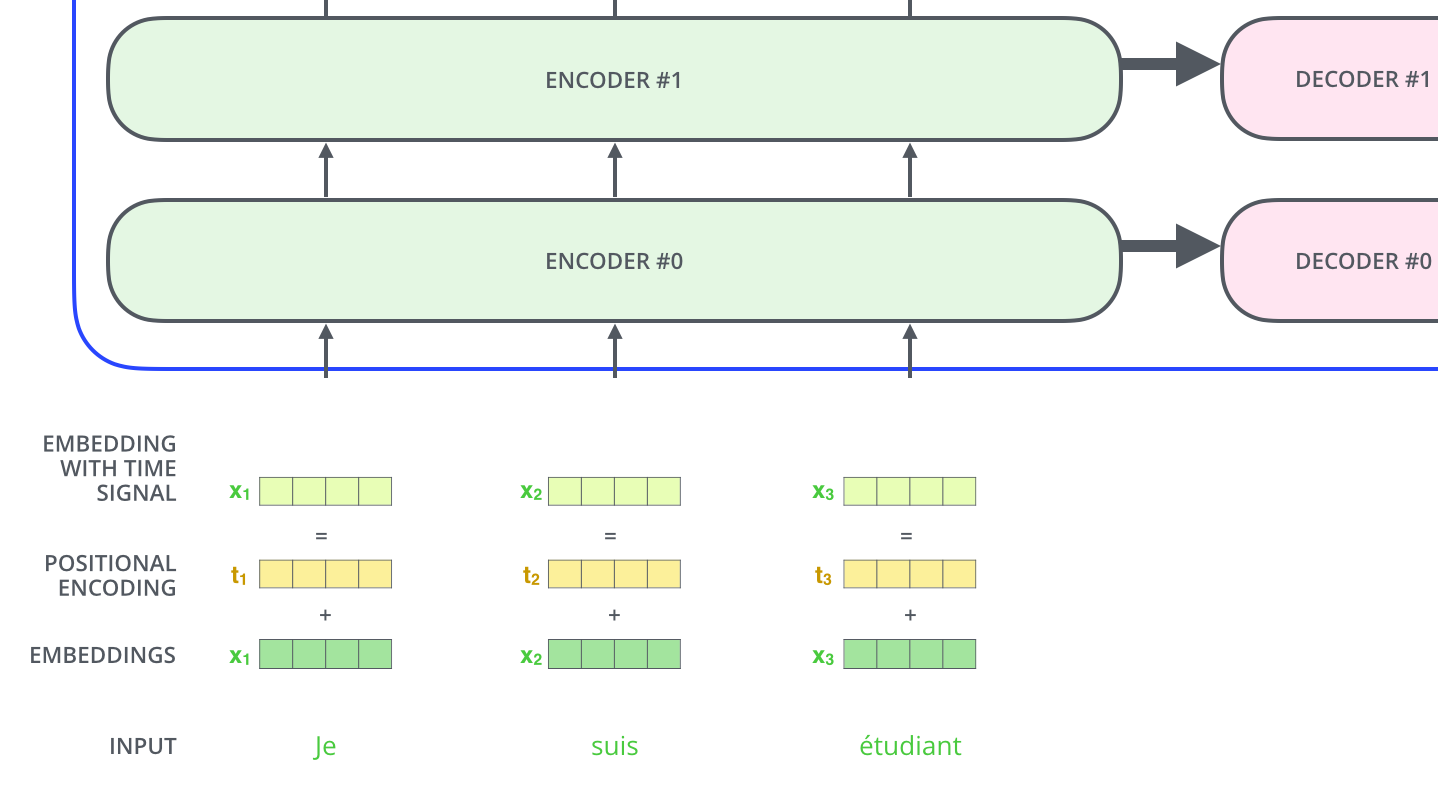
- Looks like this:
- Here we have color coded 512 sized embeddings for 20 words:
- First row is the 0th position, you can observe a pattern! There is also a split in the center, cause the values on left are generated from a function which uses sine, and the function used on the right uses cosine
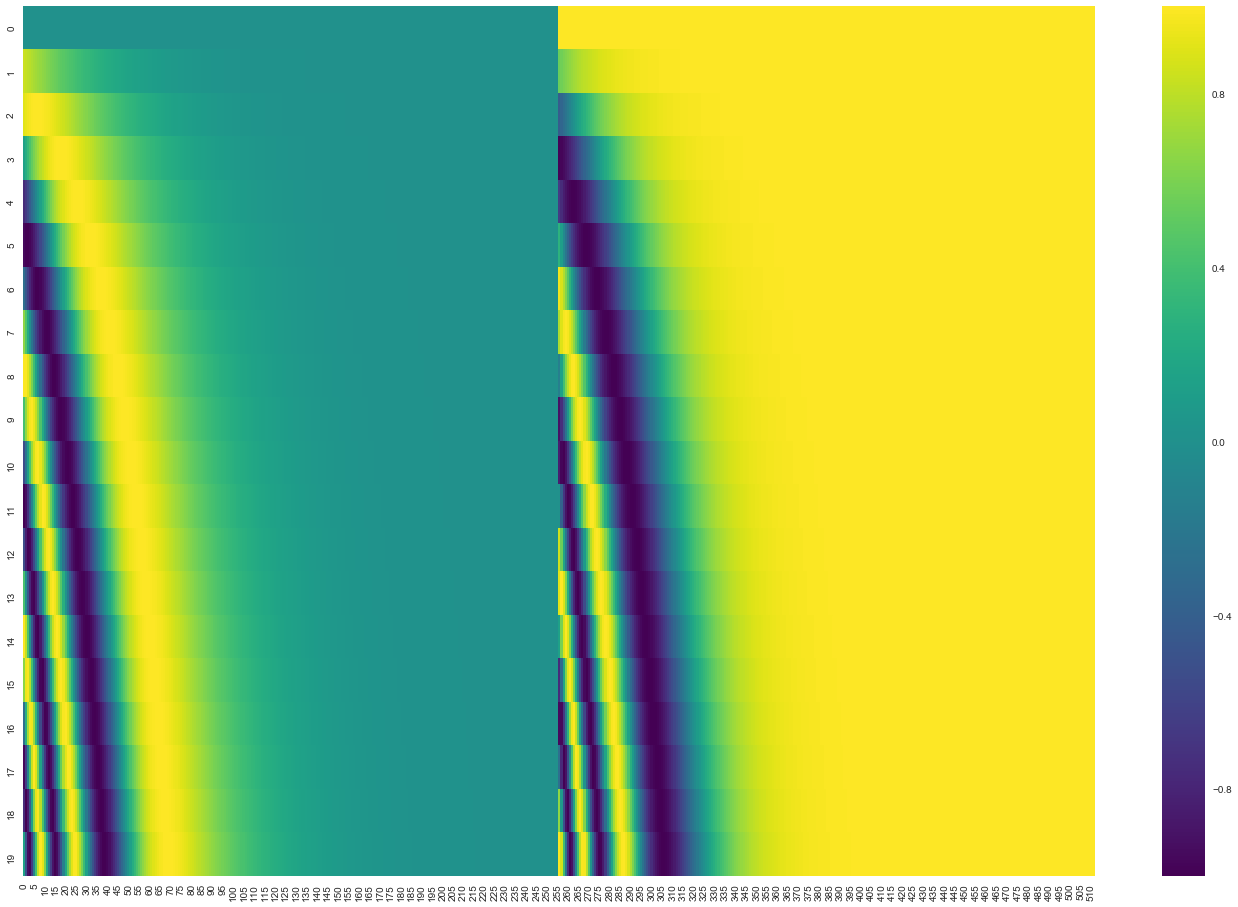
- First row is the 0th position, you can observe a pattern! There is also a split in the center, cause the values on left are generated from a function which uses sine, and the function used on the right uses cosine
- There are more things to read on this, but I don't think I am ever gonna see that lol
Residuals
-
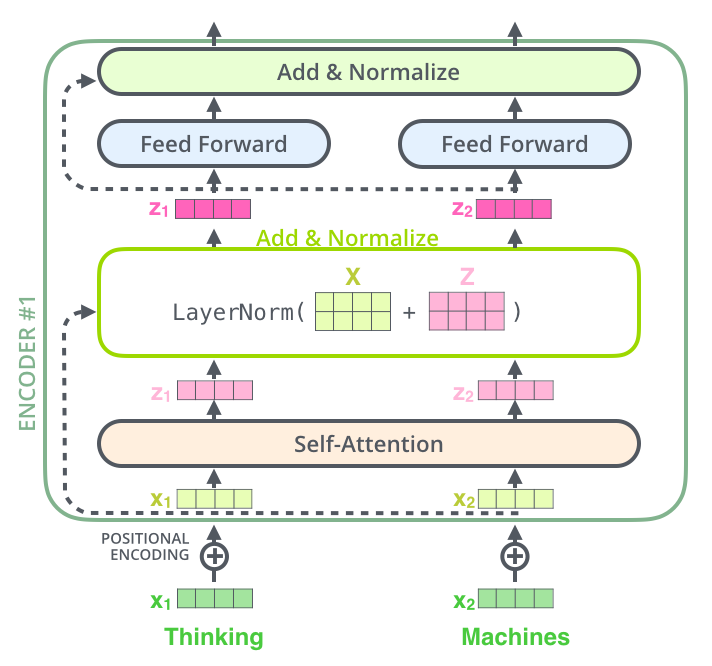
Each sublayer of self attention and feed forward layer has a residual connection around it, and it followed by a layer normalization step.
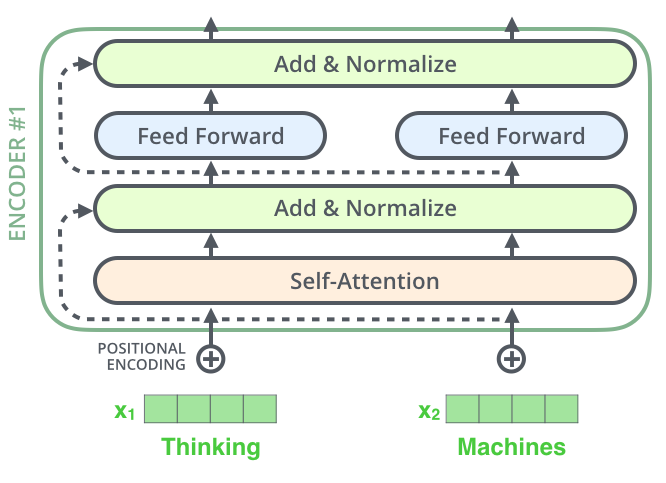
- Idk what that was lol, here's something more to look cool:
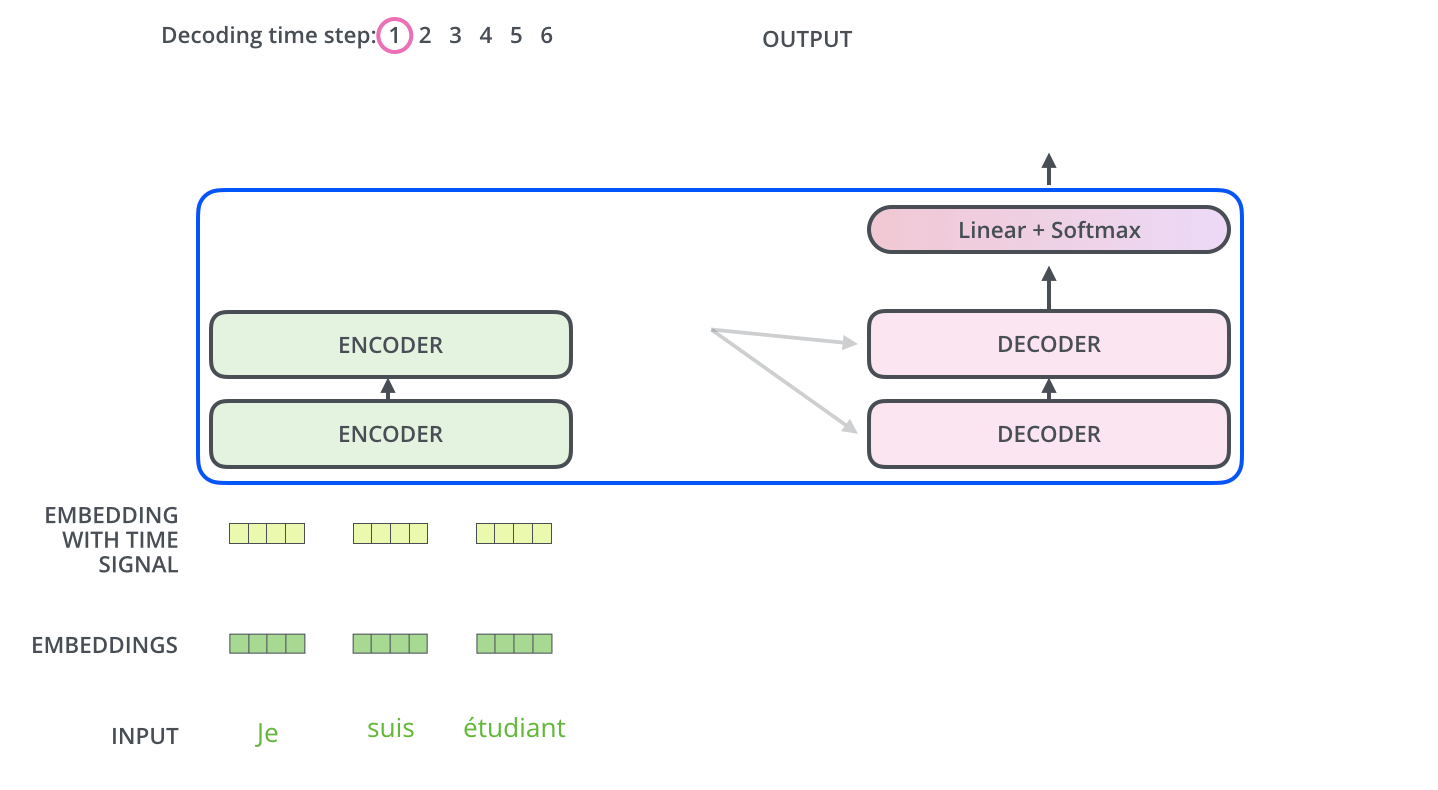
The Decoder Side:
- Encoder start by processing the input sequence,
- the output of top encoder is then transformed into a set of attention vectors K and V,
- which then are used in encoder decoder attention layer of each decoder
- So it's like this:
- and then this:
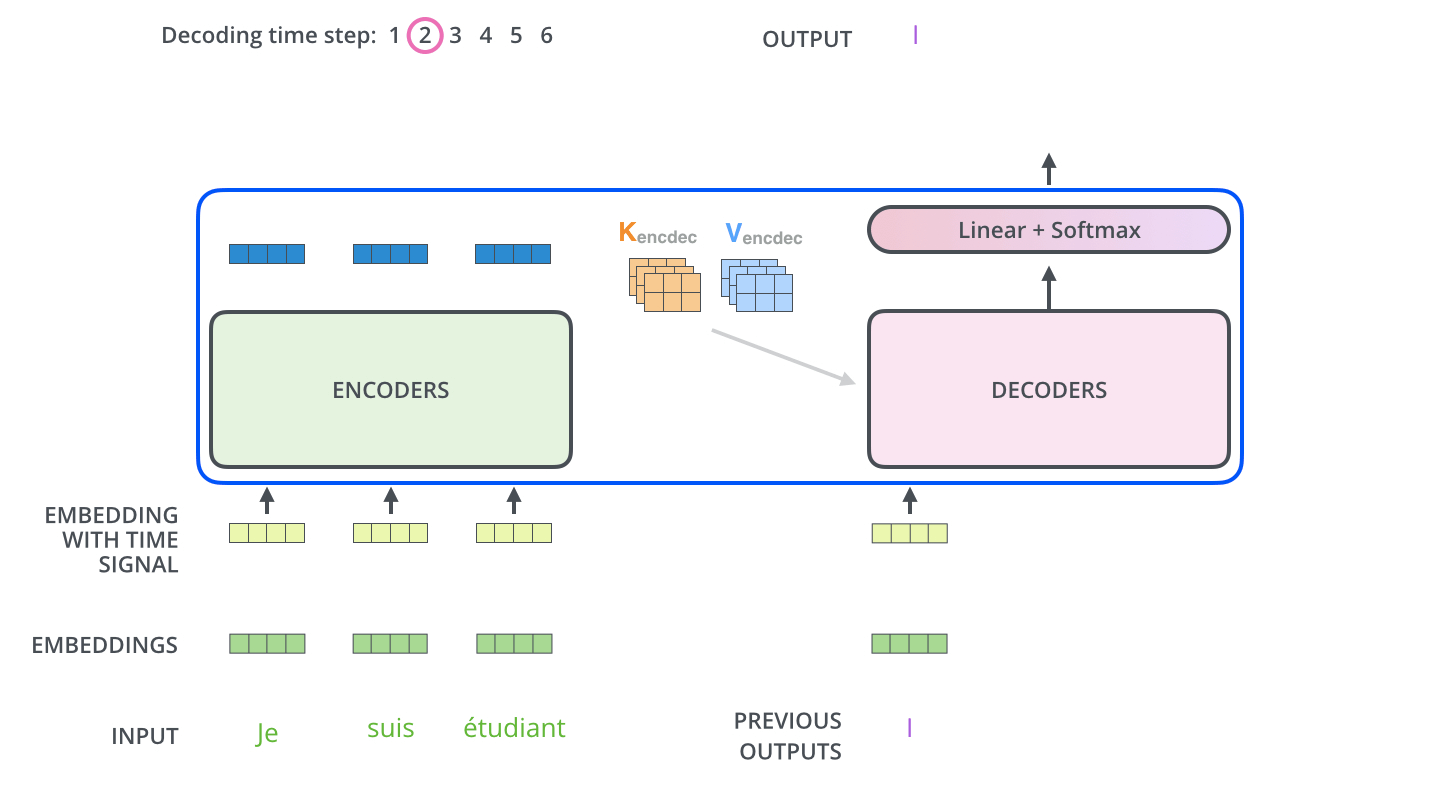
- oh it's a gif lol, check this then: https://jalammar.github.io/images/t/transformer_decoding_2.gif
- Self attention in decoder side works slightly different. It is allowed to attend to earlier positions in the output sequence? This is done by masking future positions before softmax step.
- The encoder decoder attention layer works just like multi headed self attention, just that it creates the Queries matrix from layer below it and takes the Keys and Values from the output of the encoder stack.
Final Linear and Softmax layer
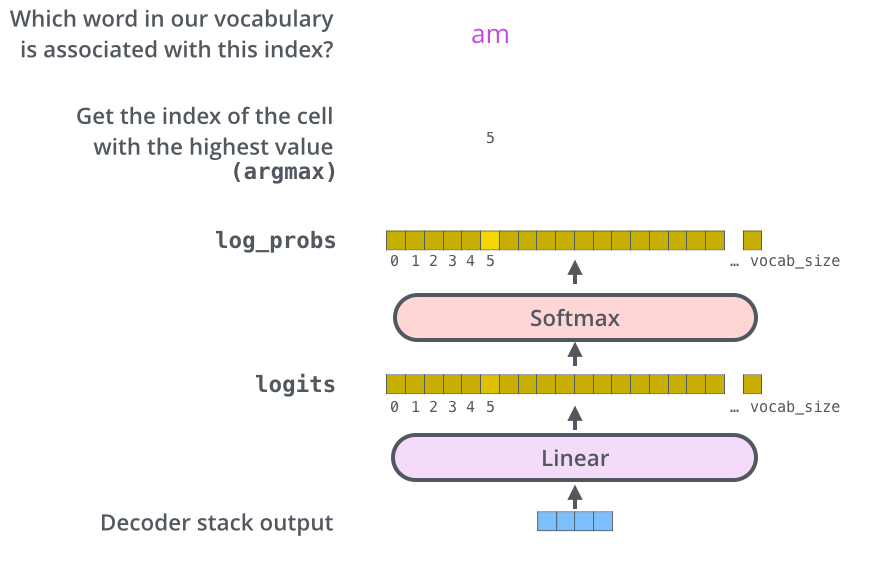
- Decoder stack outputs a vector of floats. How to make words from that? Linear layer and softmax layer handles that.
- Linear layer, a fully connected neural network, projects the vector coming from decoder stack into a much much larger vector called a logits vector.
- Say that out model knows 10,000 English words, from the training dataset, so logits vector would be 10,000 cells wide, each cell giving score to each unique word. That is the output of model after linear layer.
- The softmax layer then turns those scores into probability, cell with highest probability is chosen and the word associated with that becomes the output of the transformer.
-
Like this:
Recap of training
- An untrained model go through same forward pass, just we have labelled training dataset, so we can compare outputs.
- Say out dictionary just has these 6 words, then in 1 hot encoding we can represent "am" as this:
- one hot encoding of "am"
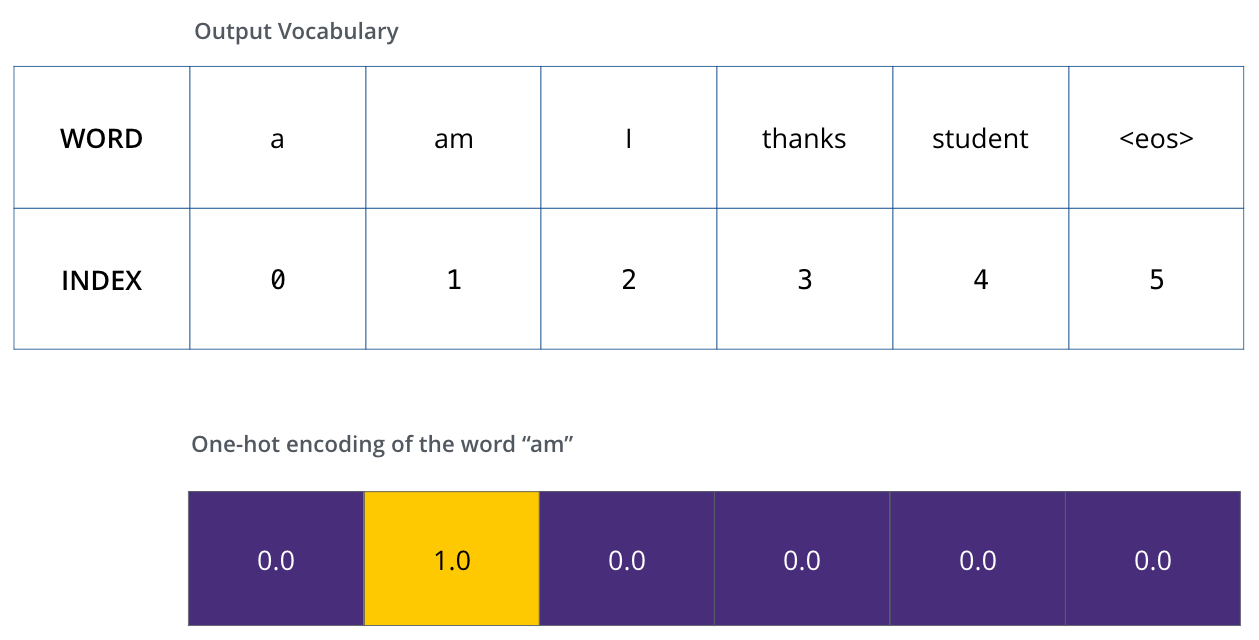
- one hot encoding of "am"
- LOSS FUNCTION is the metrics used to optimize the model to get through training phase. We use some cooler math magic which I am unaware of along with back propagation
- So post all that say we just want to train model on this small example,
- one step would look like this:
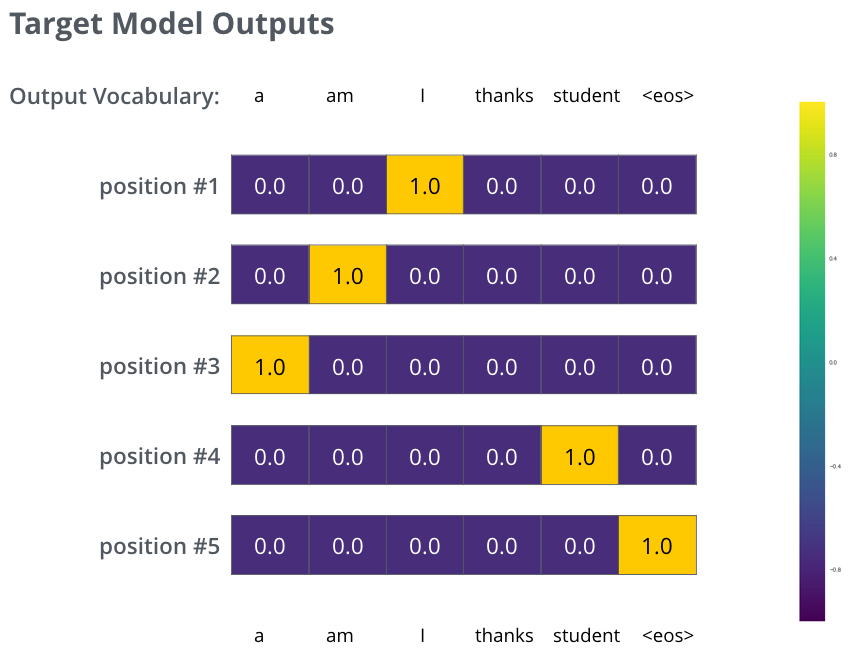
- and the final probability distributions would looks like this:
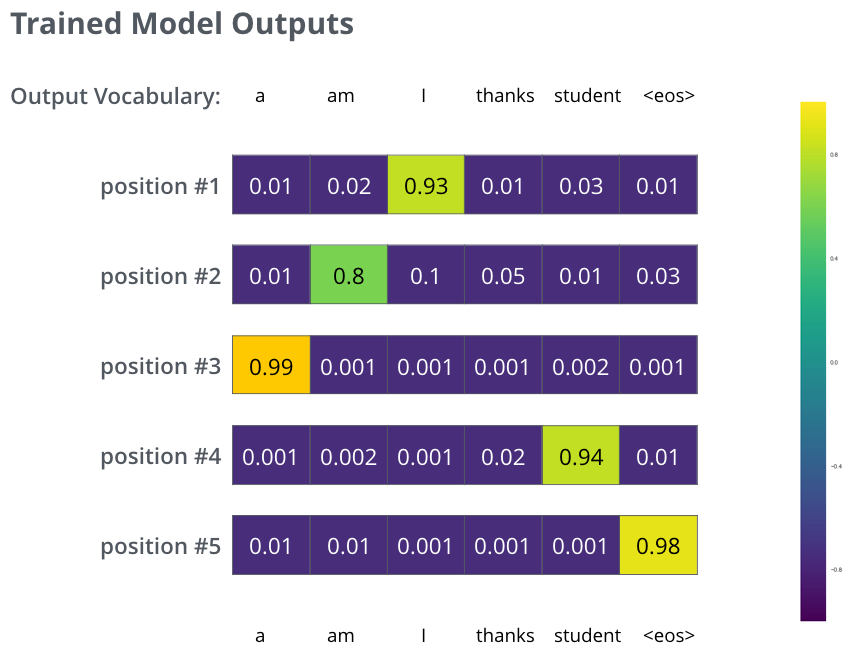
- one step would look like this:
References 📘
https://jalammar.github.io/illustrated-transformer/