Aim 🥅

Understand neural networks via an example of number detection from images. Learn about

• neuron
• activation
• layer
• weights
• biases
• neuron as a function
• neural networks as a function

TL;DR 🩳

1. We start with a task to detect a number drawn on a canvas, for detection we made neural network out of this.
   1. split the canvas on a 28 by 28 grid
   2. assign each grid pixel a number from 0 to 1 to show the color (1 for white & 0 for black)
   3. each pixel now is a neuron and the value assigned to it is called activation
   4. collect these neurons in a list, this makes our first layer of 28 X 28 = 784 neurons
   5. now we make next layers combining small parts of the pixels together to form a white color for detection in clusters sort of thing, with this we are making 16 neuron layer 2, the choise of 2 hidden layers of 16 neurons each is just for aesthetic purposes
   6. now a neuron in layer 2 can be calculated by multiplying each neuron of layer 1 by a scalar called weights, separate for each neuron, weights resemble correlation between neurons of layer 1 to layer 2, see images below and you'll get it
   7. weights can be positive or negative, resembling direct or inverse relation between neuron from layer n-1 to neuron from layer n, having negative weight to a neuron of prev layer helps finding the borders of the neuron in layer n. see the image below with red lines in the border and you'll get it.
   8. now the weighted sum here can be out of our range 0 to 1, so we use sigmoid to scale it down to 0 to 1 or to squish it!
      1. Another part of squishing is adding a bias, a bias is added to get meaningful value more out of the weighted sum, so we just add a number to the weighted sum before putting it in the sigmoid function to get the neuron value
   9. now we have layer 2 neurons calculated by the weighted sum of each neuron, we repeat it for finding layer 3
   10. one we have that in the same fashion, we jump to make layer 4, our response with 10 neurons resembling each of the numbers from 0 to 9. the value in them resemble the chances of that number being drawn in the input image
   11. In this entire thing, neuron is a number from 0 to 1, or it's a function that maps all the neurons of the previous layer to a number between 0 to 1
2. Neural network is just a function! a complex function which takes in 784 params and throws out 10 values showing which number has what chances of being in the image represented by the 784 params.
3. We do not discuss how to assign the weights here, just how they work and idea around it. Calculation of weights is done in the next chapter.
4. Motivation behind the 2 hidden layers was the first hidden layer (or layer 2) should identify the edges, and the second hidden layer (or layer 3) should identify the patterns like loops/lines, while the output layer would just associate the layer 3's activated neurons to some number. FROM THE FUTURE: THIS IS GOING TO CHANGEEEE!
5. For Squishing function, ReLU - Rectified Linear Unit is better than Sigmoid.
   1. relu(x) = max(0,x)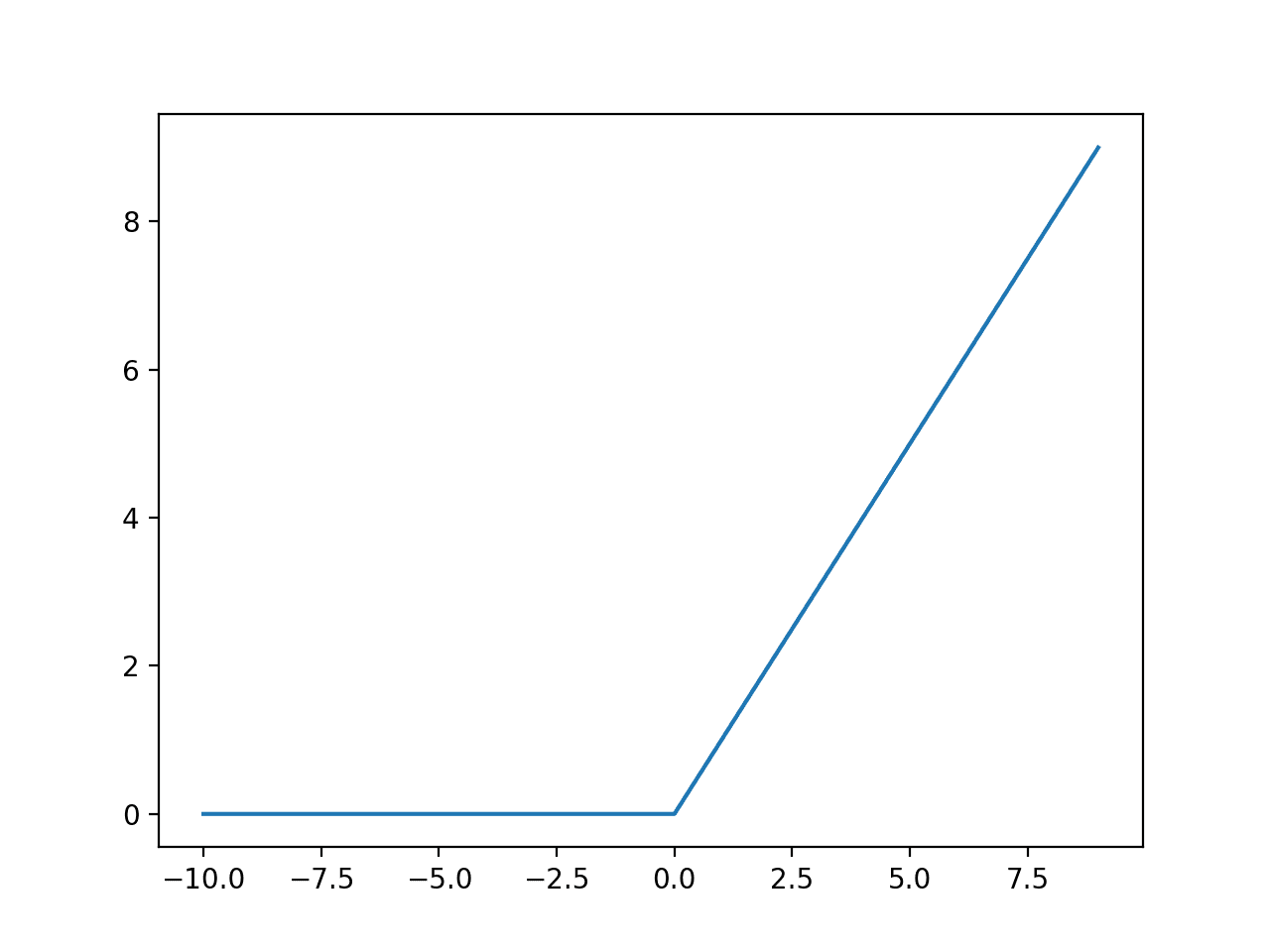
   2. While sigmoid was

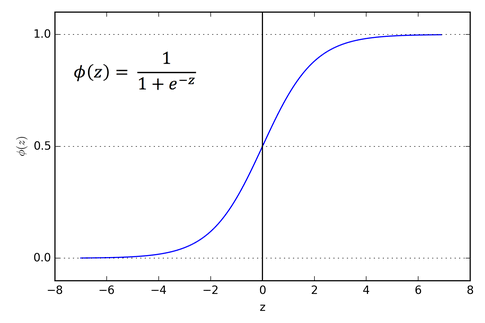
What's on the plate 🍽?

• Already discussed in [[000 Deep Learning and Neural Networks]] note, but let's discuss it all again, cause 3 Blue 1 Brown is cool

• Our task is to detect which number is written here, quite simple for humans, but idiotic machines need a 28 by 28 grid representation and a whole lot of neural networks to make it all work. Let's dig deeper!

  • There are many variants of neural networks: convolutional neural networks (CNN), recurrent neural network (RNN), transformers and many more.

  • Neuron is core of the neural network, a neural network is made up of many neurons

    • A neuron is just a number from 0.0 to 1.0 which represents the value of activation energy of that neuron
      • 0 means black and as we increase the white increases, so the borders of number would have values like 0.3 0.5 etc..
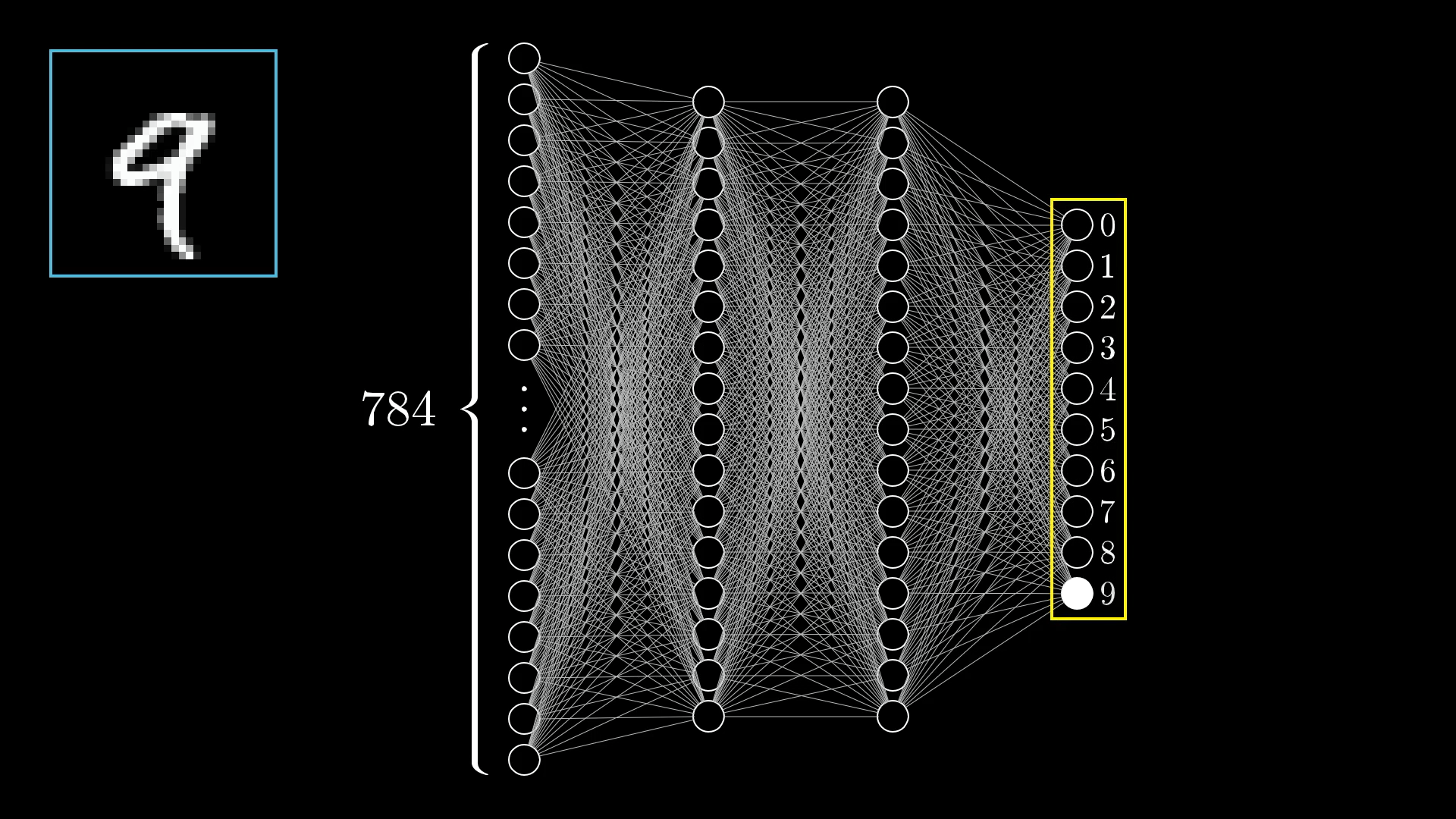
    • Now for representing a number's image, we want to use a 28 by 28 grid, that means we would have 784 neurons in our first layer. Each row has 28 neurons and we just take them all in for our input layer. We can take in the pixel color as our neuron's activation energy.
    • Each neuron represents a single pixel

  • So the process now looks like this with first layer of 784 neurons, some hidden layers and a last layer of 10 neurons where we have neurons representing probability of the input being which number

  • Hidden layers: Where the magic happens!

    • Let's take a step back and see how these layers are connected. Each neuron from first layer is connected to each neuron from the next layer with a little line, this line represents the weights, or "influence" each neuron has on the neuron of the following layer.

    • Taking another step back, let's see why these random layers work in the first place?

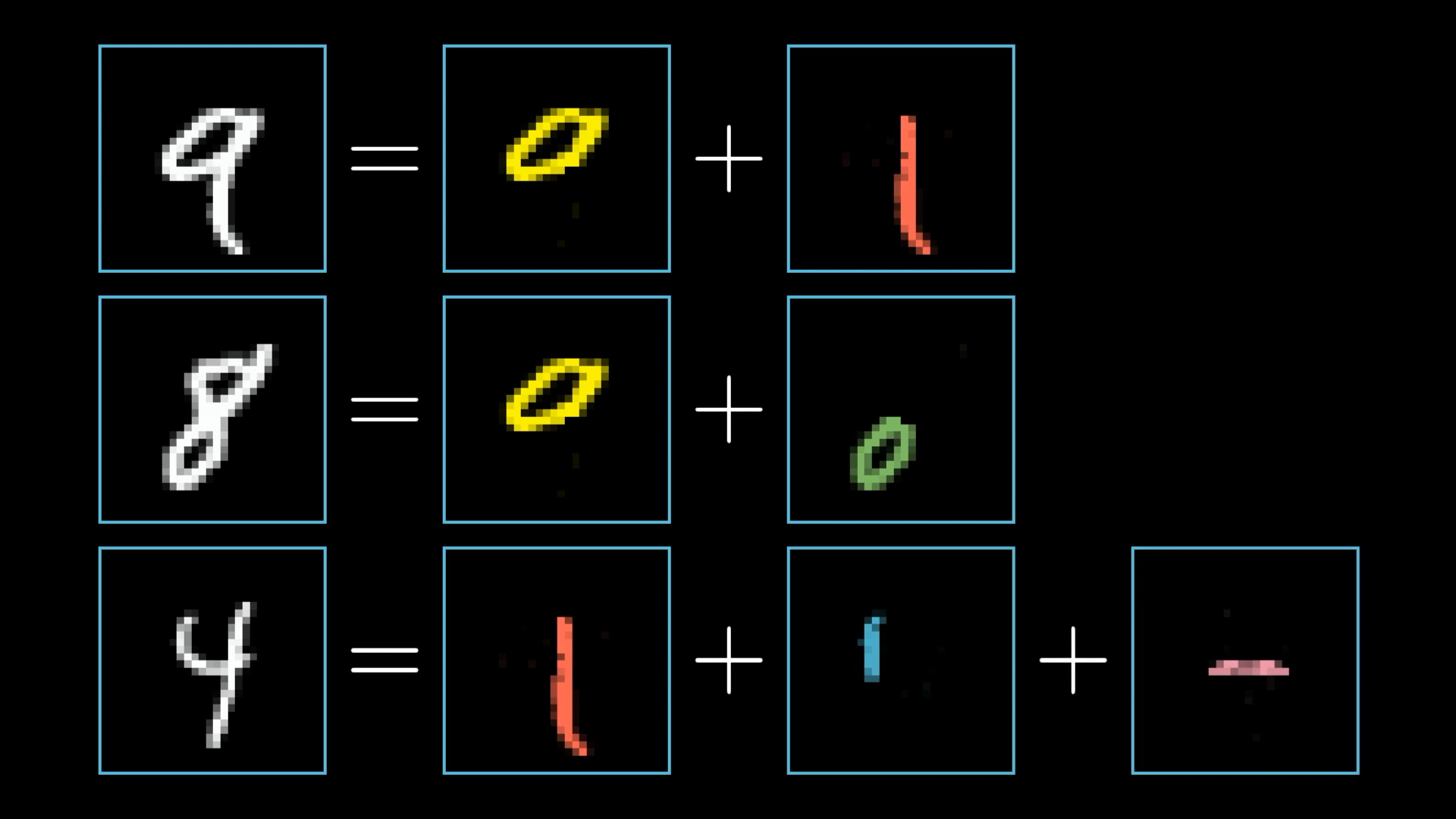
      • Each drawn number can be broken down like this in parts:

      • We broke down the image of a number in various components viz lines and loops, let's use this idea to make our second last layer now:

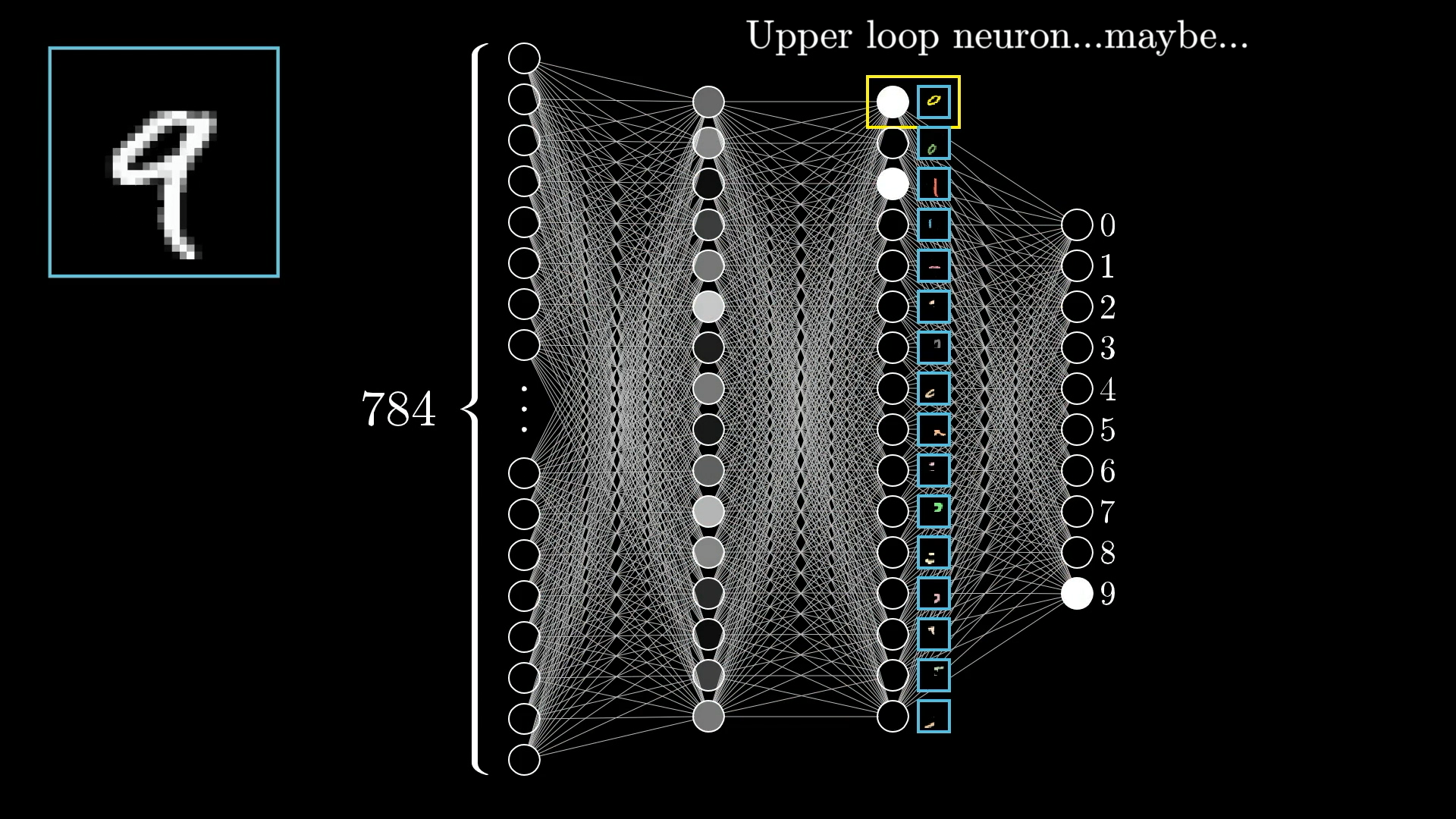
        • You can notice how a loop (1st neuron on the second last layer) and a big line (3rd neuron) are having bright colors, meaning it might just make 9 based on the penultimate image

      • Well now we can make the layer before this, i.e. third last or the second layer, where we break down even these components like loops into sub components

        • and a line can be broken down to these sub-components

      • Now layers are to break down our complex image(problem) to smaller fragments for better understanding

      • Beyond image recognition, audio recognition also follows the same layered approach

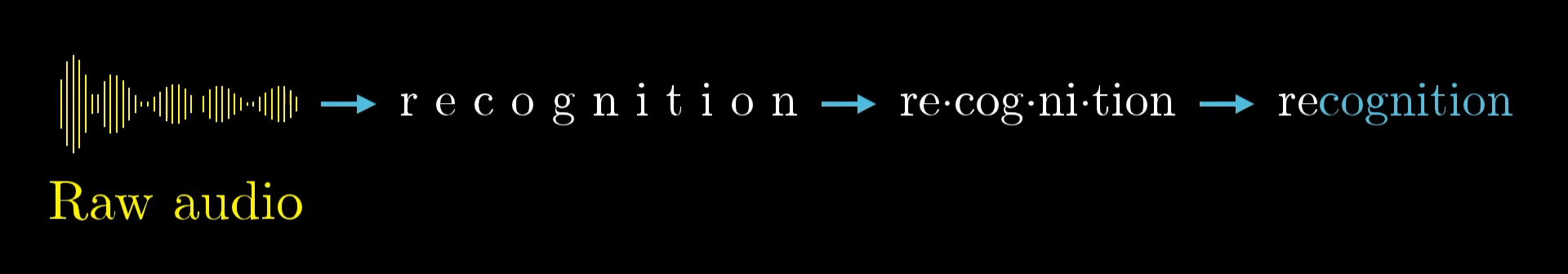
      • Motivation behind the 2 hidden layers was the first hidden layer (or layer 2) should identify the edges, and the second hidden layer (or layer 3) should identify the patterns like loops/lines, while the output layer would just associate the layer 3's activated neurons to some number.

    • Now we can go back to how the information propagates between layers

      • For example, let's take this neuron from second layer which represents this white region in the image, now can we somehow find out neurons from the first layer which contribute (or influence) this neuron in the second layer which resembles this image?!
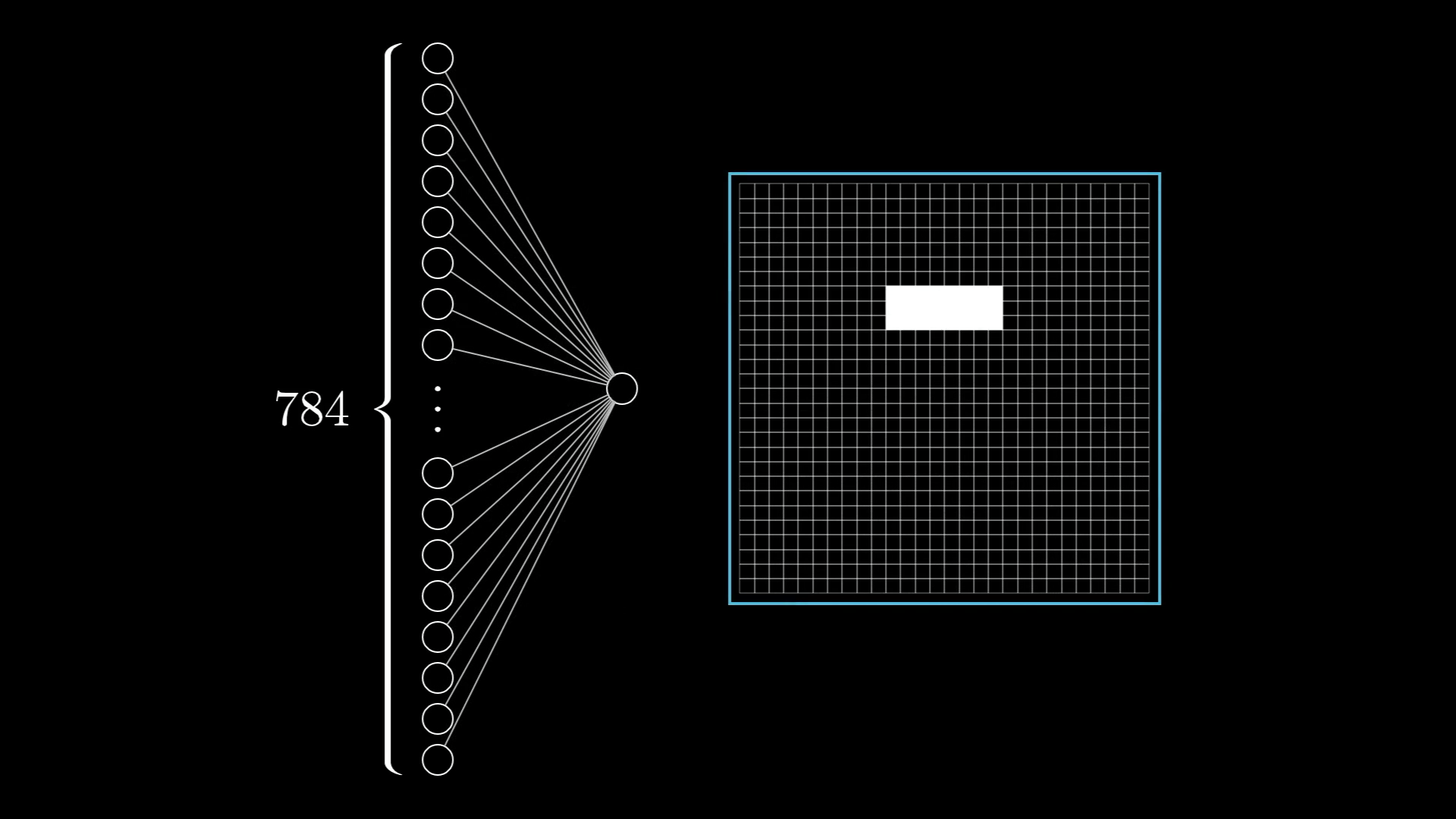
        • We can assign weights to each connecting line between neurons of first layer to this selected neuron of the second layer and it would be something like this:
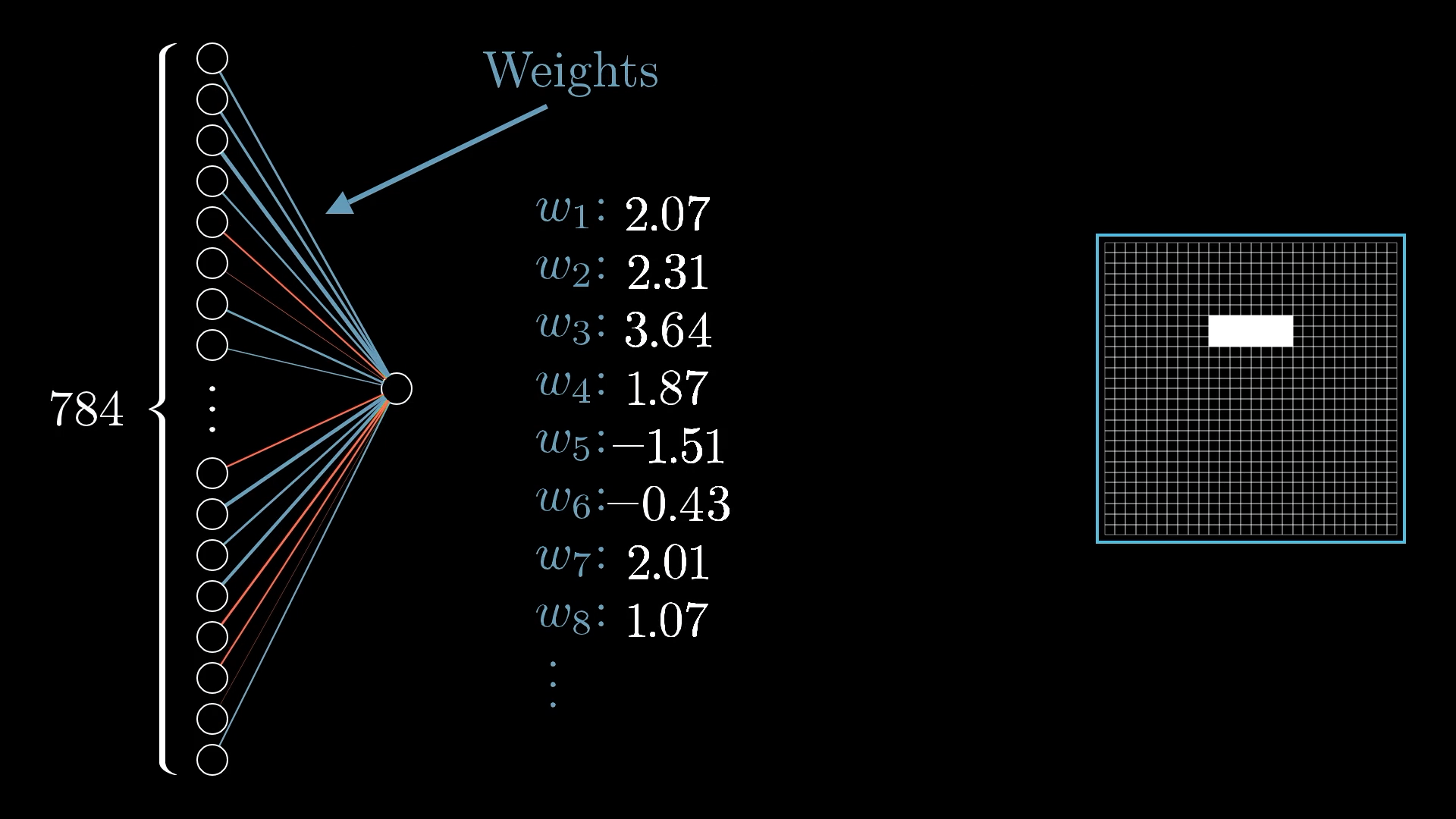
        • So we would have weights of the edges, and activation energies of the neurons of the first layers combined to detect the activation energy of the selected neuron in the next layer: w₁a₁ + w₂a₂ + w₃a₃ + w₄a₄ + ⋯ + wₙaₙ
        • Now how to calculate these weights?
          • Again weight is just a number denoting the correlation between the neuron of the second layer and the neuron of the first layer
            • if neuron of first layer is on:
              • positive weight → neuron of second layer should also be on (positive influence, badho to badho) (blue pixel)
              • negative weight → neuron of second layer should be off (negative influence, inverse relation) (red pixel)
        • So now for all these 784 neurons of the first layer, there should be 784 weights to connect to each of the neuron of the second layer, and these weights can be a grid (list) for simplicity
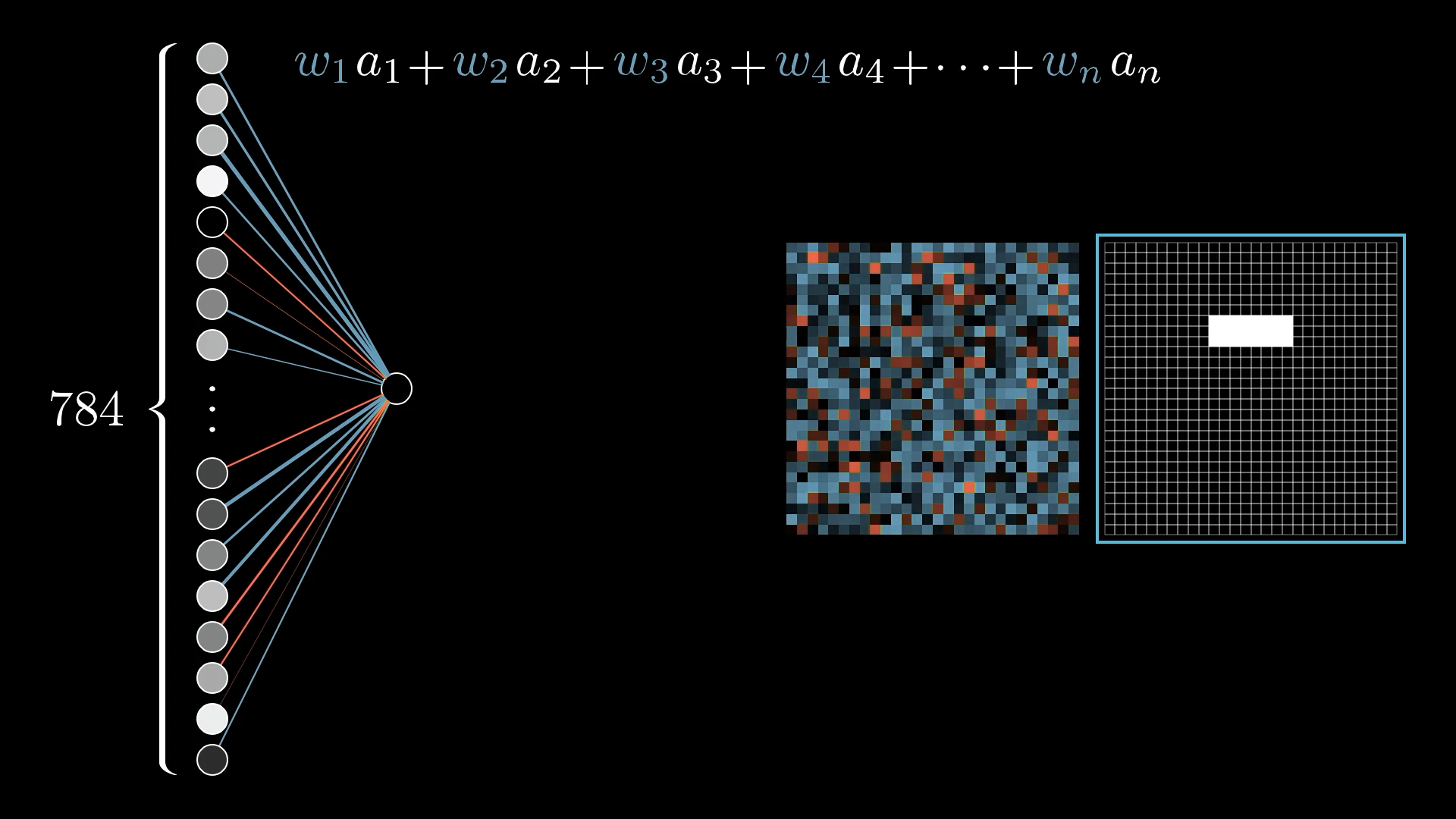
        • Now we know blue means on or closer to 1, so if we want to detect the neuron from second layer with the white region, can we just turn off all the other neurons and just turn on the neurons which are overlapping (or forming) the selected white region
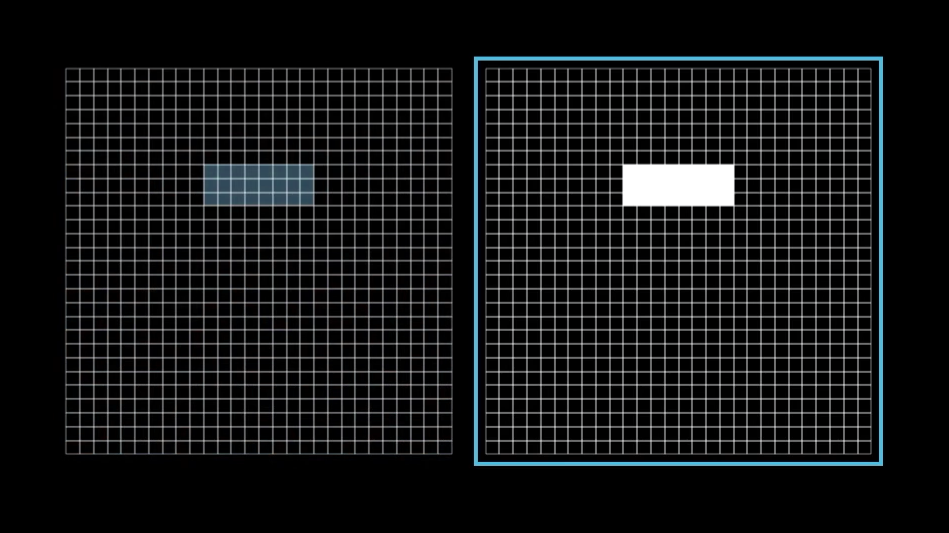
        • Now this is fine, but negative weights in red are very important, they can help us remove the borders, so we make it like this so we get more refined border, as red region around the borders indicate that the values on border are 0, thus in the second layer there is a strict boundary on the borders like this
        • "By adding some negative weights above and below, we make sure the neuron is most activated when a narrow edge of pixels is turned on, but the surrounding pixels are dark."

    • Sigmoid Squishification

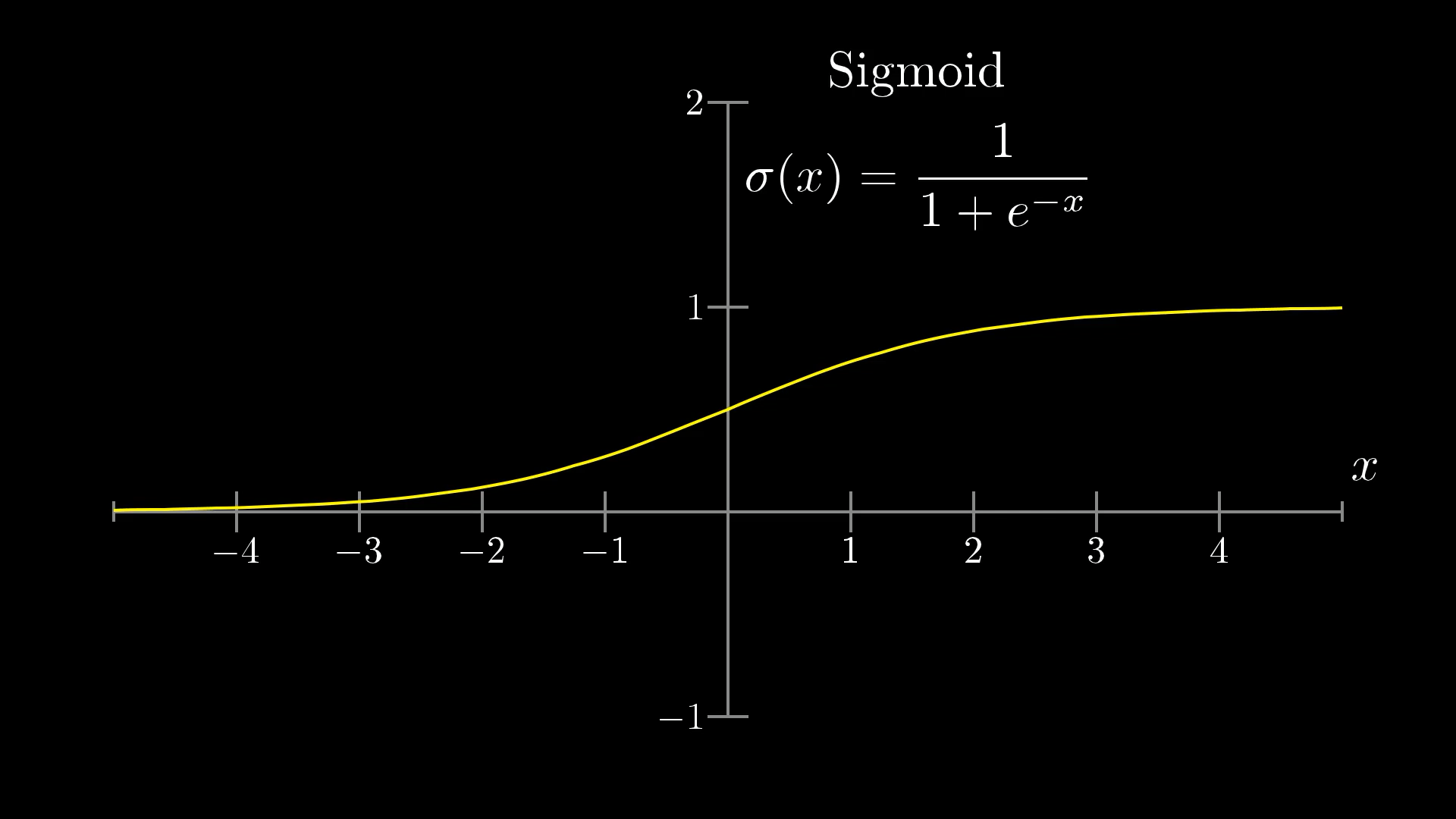
      • Now these values coming from the sum of weights × activation energy is going to be out of the range 0 to 1, so we introduce a squishification function (to squeeze the results to the range 0 to 1) called sigmoid or logistic curve.
      • Sigmoid just does this:
      • Sigmoid is like this (so if x is negative → then go close to 0, if x is 0 → then just 1/2, if x is positive → then go close to 1)
      • Now the weighted sum for next neuron can be very low, and that would be meaningless for us, so we can add some "bias", or add a number to weighted sum before throwing it into the sigmoid function, like this:
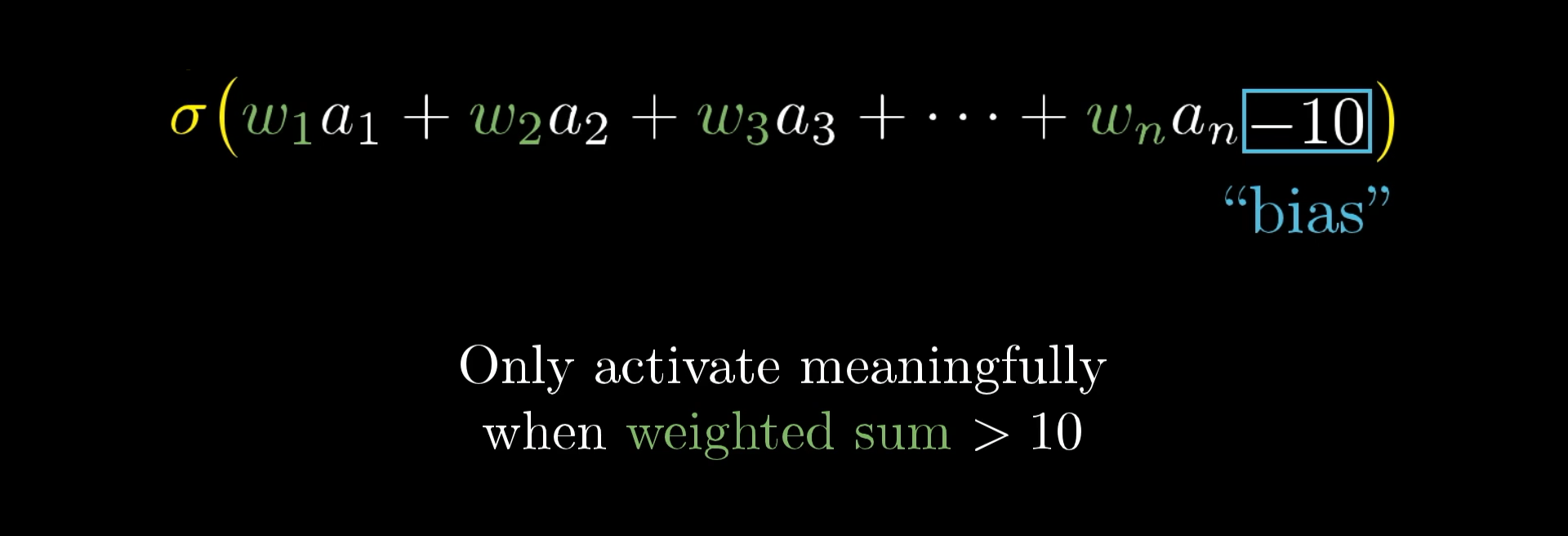
      • So
        • weights: what pixel pattern the neuron is going to pick up
        • bias: tells how big the weighted sum needs to be before the neuron gets meaningfully active

    • Now there are more neurons, for 16 neurons second layer, that’s 784×16 weights and 16 biases. That's just for the second layer, in total there would be 13,002 knobs and dials or total weights and biases

      • we don't set them all up, that's where the learning comes in. but it is interesting to note how it really works under the hood in the hidden layers

    • We can now do more compact notation for our neurons:

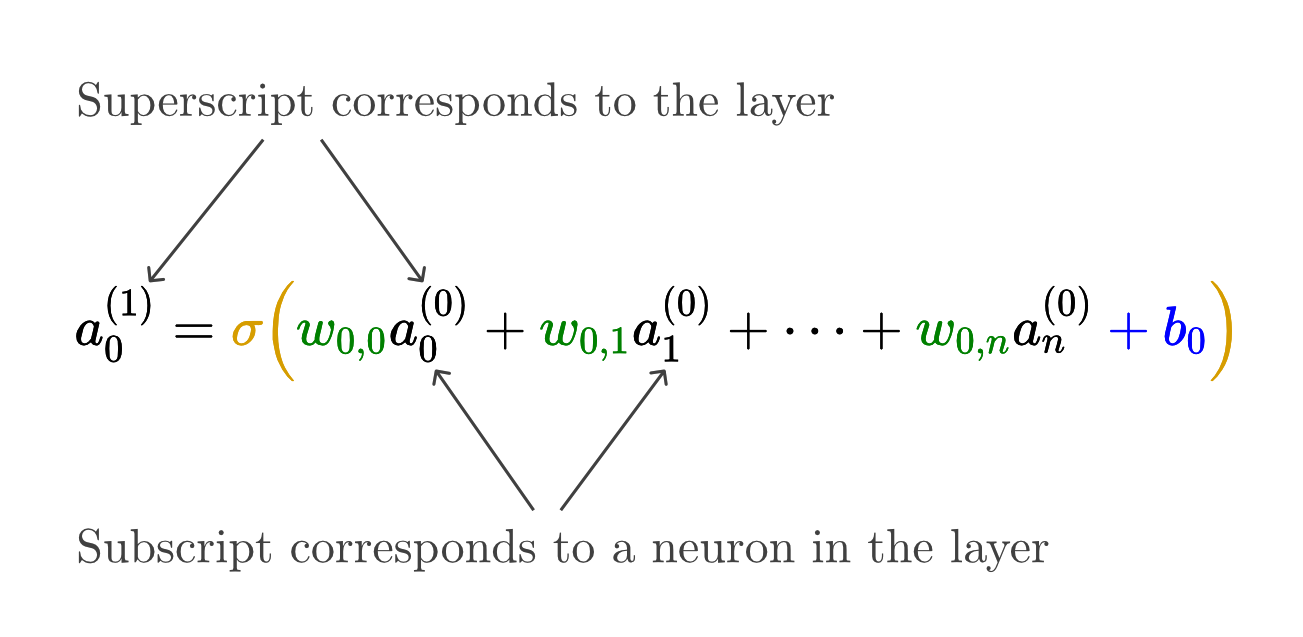
      • we can also use matrix multiplication now to simplify all this mess
        • So it can be just this
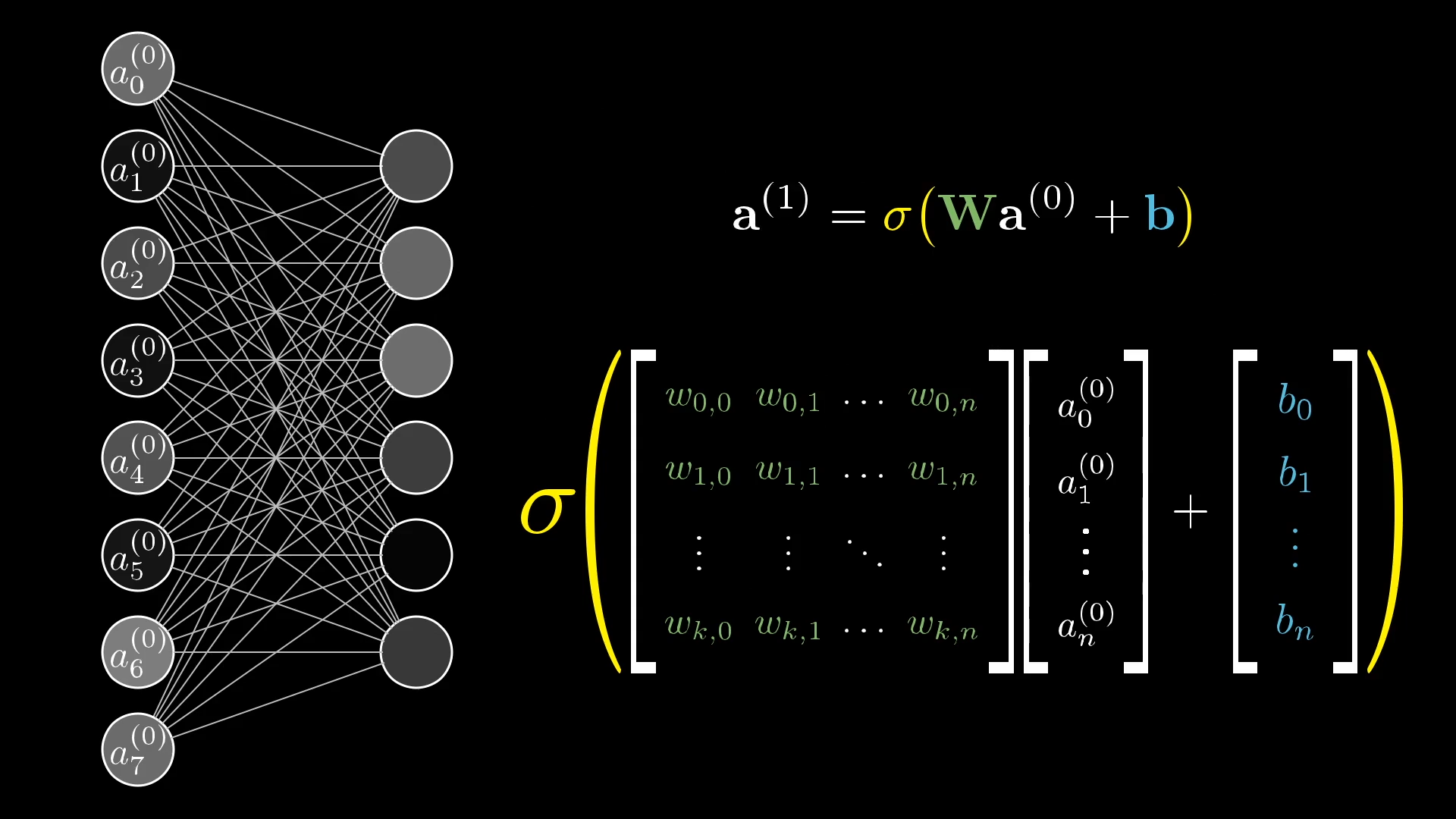
        • That's why the matrix calculations matter a lot!

    • Earlier we said to consider neuron just as a number between 0 and 1, rather neuron can be thought of as a function which map activation of previous layer to a number between 0 and 1. And this entire network then is just a function! A function that takes in 784 params as input and throws out 10 outputs, also covering total 13k params in operations, still it's just a function!!!

References 📘

• 3Blue1Brown - Neural Networks